Le paradoxe de Simpson tire son nom du statisticien Edward Simpson.
Il explique comment on peut obtenir des conclusions complètement foireuses d'une statistique tout à fait exacte SI on a fait des "bêtises" (volontaires ou involontaires) au départ ...
Pour que le paradoxe se produise, il faut 2 ingrédients :
- Premièrement il faut une variable qui influe sur le résultat final, et qui n’est pas explicitée au départ. On appelle cela un facteur de confusion.
- Deuxièmement, il faut que l’échantillon qu’on étudie ne soit pas distribué de manière homogène .
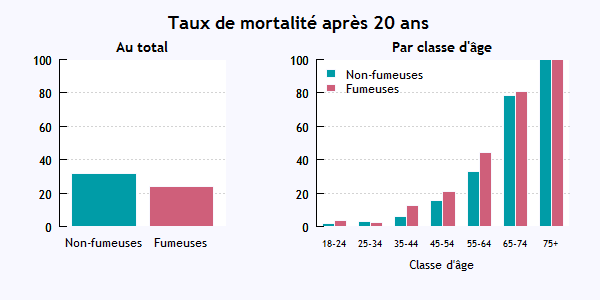
Fumer, c’est bon pour la santé... chiffres en main !
Dans cette étude, 1314 femmes ont été suivies pendant 20 ans, et l’objectif était de comparer le taux de mortalité des fumeuses et des non-fumeuses.
Après 20 ans, le taux de mortalité chez les fumeuses était de 24%, alors que celui des non-fumeuses était 31%. Alors, est-ce que non-fumer tue ?
Examinons les chiffres de plus près.
Dans l’étude globale , il y avait 582 fumeuses et 139 sont mortes (cela fait bien 24%), ainsi que 732 non-fumeuses dont 230 sont mortes (31%, pas de problème).
Par contre,là où le paysage change, c’est quand on représente ces chiffres en séparant par classe d’âge. C’est ce que montre le graphique ci-dessous .
Comme vous le voyez, si on raisonne par classe d’âge, dans chaque tranche la mortalité chez les fumeuses a été supérieure à celle des non-fumeuses. On est rassurés.
Mais comment les chiffres peuvent-ils s’inverser quand on groupe tout le monde ?
Peut-être avez vous senti ce qui cloche :
1° dans la population initiale, il y a beaucoup plus de femmes âgées non-fumeuses que fumeuses.
2° dans chaque tranche d’âge les fumeuses meurent plus .
3° mais les agées meurent de toutes façons beaucoup plus que le jeunes, qu'elles fument ou pas .
4° comme il y a beaucoup plus d'agées que de jeunes ds l'étude,au final l'essentiel des morts sera du à l'âge et pas au tabac .
Cette étude ne veut rien dire ...Mais il n'y a que vous qui le savez .... Sauf si vous publiez vous sources ... mais qui ça intéresse ?